1.1 Vectors and Linear Combinations

[1] Column vector (열 벡터)

(1) 벡터 성분을 열 방향(세로)로 배열한 행렬을 의미한다. n차원 열 벡터는 n by 1 크기의 행렬이다.

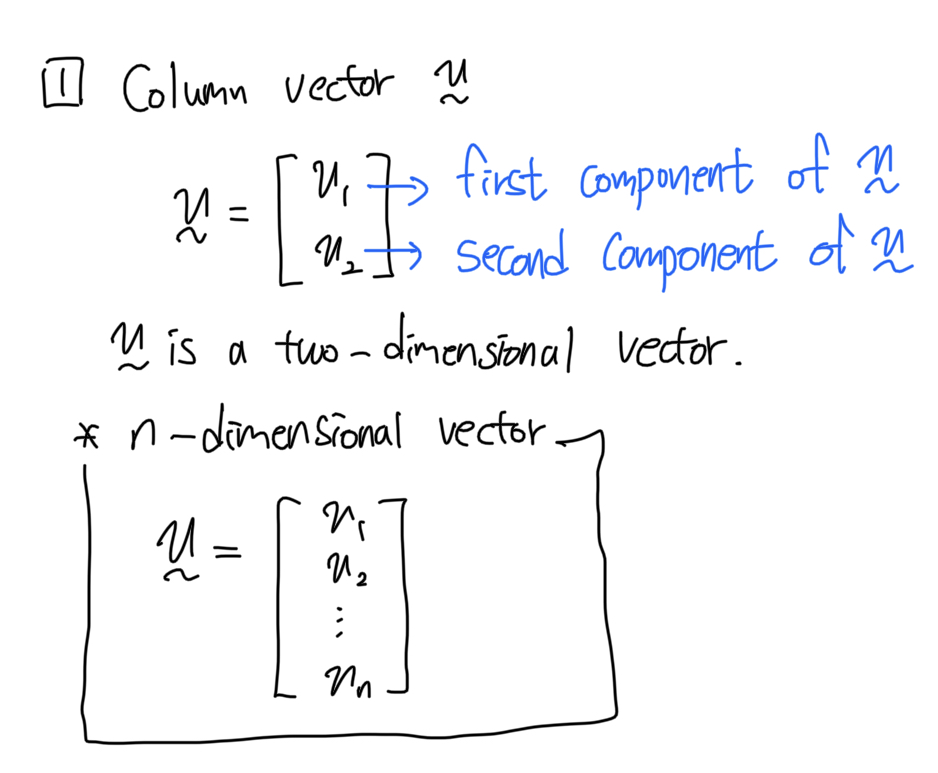
(2) 행 벡터(row vector)는 벡터 성분을 행 방향(가로)로 배열한 행렬이며, 열 벡터를 전치(transpose)한 형태와 동등하다.

---

[2] Vector addition (벡터 덧셈)

(1) 벡터의 덧셈은 동일한 위치(배열)를 갖는 성분 간의 덧셈 연산을 취한다.

(2) 뺄셈의 경우도 (1)과 동일하다.

(3) 다른 크기의 벡터 간의 덧셈은 불가하다.

---

[3] Scalar multiplication (스칼라 곱)

(1) 벡터에 스칼라 상수를 곱한 결과는, 각각의 성분에 스칼라 상수를 곱한것과 같다.

---

[4] Zero vector (영 벡터)

(1) 영 벡터는 벡터 성분이 모두 0인 벡터를 말하며, 숫자 0과는 엄연히 다르다.

---

[5] Linear combination (선형 결합)

(1) 벡터의 선형 결합은 스칼라 곱을 취한 벡터들을 합하는 것과 같다.

(2) 위의 그림에서 임의의 스칼라 c,d,e로 인해 형성되는 모든 선형 결합의 결과는 무엇일지 고민해보자. 만약 모든 벡터가 영 벡터라면, 선형 결합의 결과는 당연하게도 영 벡터이고 이는 매우 극단적인 케이스로 분류할 수 있다. 하지만, 영 벡터가 아닌 임의의 벡터들 간의 선형 결합 결과는 원점(0,0,0)을 지나는 line(1차원), plane(2차원), space(3차원)이 될 수 있다. 물론 종속관계의 벡터가 있다면 3개의 벡터간의 선형결합이라도 space를 형성하지 못할 수 있다. 보다 자세한건 관련 챕터에서 다루자.